7_B+Tree Indexes
7-B+Tree Indexes
7.1 B-Tree Family

7.1 Tree Indexes
DBMS 在执行查询的时候,更多是查询索引而不是查询数据库中的表
索引问题
存储开销
维护索引开销
7.2 B+ Tree
是一个自平衡树。这是一种插入、删除均为 O(log n)的数据结构。可以支持线性遍历(哈希表不能做到)
相比 Hash Table,最好的性能是 O(1),最差时退化到 O(n)。因为平衡,所以任意一个叶子结点到根结点的时间复杂度均为 O(log n)
对于读写磁盘上整页数据具有其他数据结构不具备的优势
7.2.1 B+ Tree Properties
$M$阶搜索树
- $ \frac{M}{2} - 1 \le keys \le M - 1$
- 每个中间结点,$k$个关键字有$k+1$个非空孩子
- 叶子结点存放关键字和数据

Node
key 继承自索引依赖的属性
value
inner node 中 value 是下一个节点的指针;leaf node 中是存放数据的地址或者数据本身
所有的 NULL 值要么存放在 first leaf node,要么是 last leaf node
Leaf Node
常见的叶子结点具体实现如图所示:

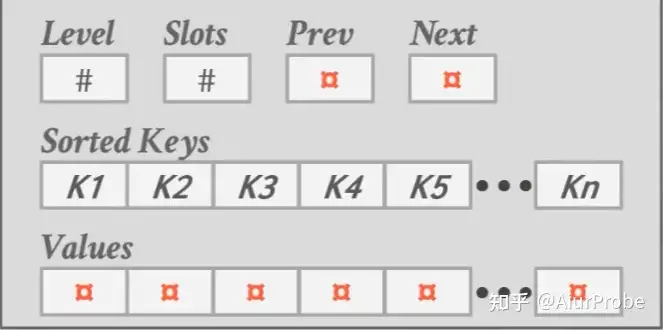
B-Tree VS. B+Tree
将 key 数组和 values 分开保存而不是放在一起保存,是因为查询时常需要扫描大量 key,key 的长度固定,有助于 CPU cache hit;
查询时只需要扫描 key,就不用在缓存里读取 value 的信息。当查询到具体的 key 时,通过 offset 能够直接找到 values 数组中的值。
leaf node value
- Record IDs
存放 tuple 的指针
- Tuple Data
直接存放 tuple 的内容
B+树 Insert / Delete
Insert

Delete

7.2.2 B+ Tree Selection conditions
只有少数系统支持前缀查找及后缀查找
$Find \ Key=(A,B), Find \ Key=(A, )$;很多数据库不支持匹配$Find \ Key=(, B)$;该查询可能需要遍历整张表


7.2.3 Duplicate Keys
append recordID: 联合主键(<key, (page, slot)>)
overflow leaf nodes: 外接一个溢出(overflow)叶子结点;将重复的键放置在溢出叶子结点上

7.2.4 clustered indexs
- 数据按照主键索引来组织
- 索引与文件一一对应,对于线性遍历有好处

非聚簇索引,遍历可以优化
扫描叶节点不立即检索元组,而是找到它们后再进行检索

7.2.5 Node size
慢速设备 B+树结点应该设计的越大,一次 IO 读回的数据越多
高速设备 SSD 或 Main memory 应该设计的更小,不需要太多的冗余数据
结点的大小也取决于负载
AP 型数据库:Leaf Node Scans 大节点
TP 型数据库:Root-to-Leaf Traversals (点查询) 小节点

7.2.6 Merge Threshold
可以通过调整阈值来延后分割/合并操作
7.2.6 Variable-length Keys
- 存放 Key 的指针
大量非顺序 IO 操作,查找成本太高
- 使用变长结点
- Padding
- Key Map / Indirection
在结点内部使用指针来对应 KV

7.2.7 Intra-Node Search
- Linear:从开始到结尾线性搜索;使用 SIMD 进行向量化比较

- Binary:二分查找
- Interpolation:推断需要查找关键字的位置(单调递增且无间隙)

7.2.8 Optimization
Prefix compression
前缀压缩——存放在相同叶子结点中的数据应该具有相同的前缀
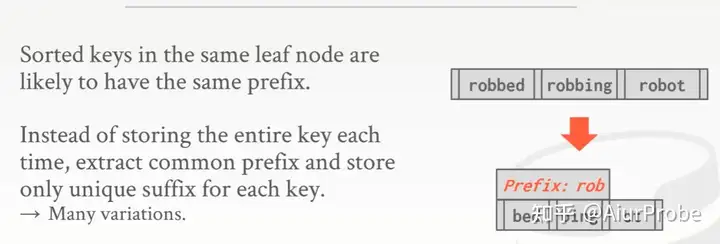
Deduplication
将冗余的键压缩

suffix truncation
后缀截断
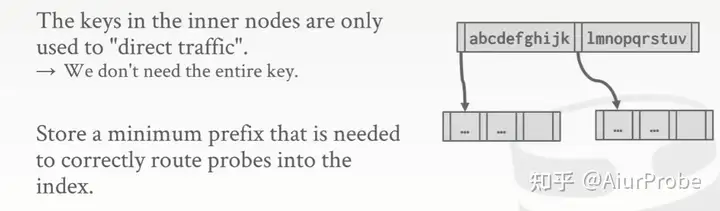
当用于确认方向的路标很长,但是迥然不同时,也没有必要存完整的 key,abcdefg…存储为 abc,lmnopq…存储为 lmn 即可。这种方式在树不会经常改变时很有用,总体上用的比前缀压缩要少。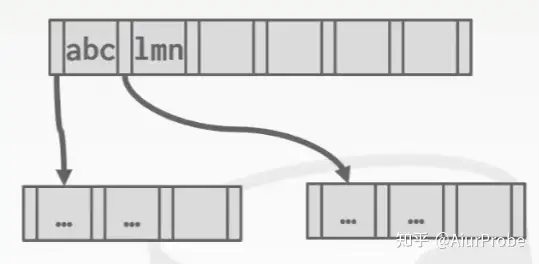
bulk insert
批量插入
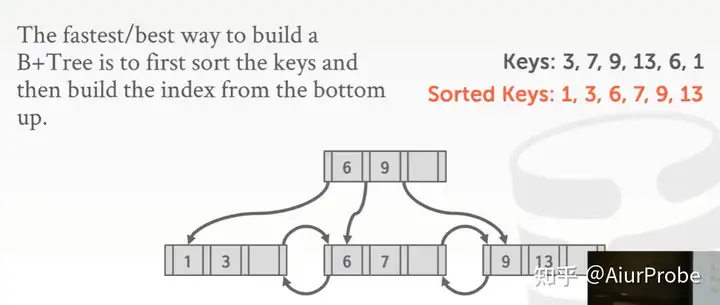
当提前知道需要插入的所有 key 时,可以预先对 key 们排序,然后自下而上地构建整颗树。这很快。
pointer swizzling
存放页指针而不是页号

当确保需要遍历的结点所在的 page 都被 pin 在 buffer pool 中时,结点间指针就不用再(仅)存 page id,而是可以直接(额外)存原始指针,遍历这些 node 时就能避免去访问 buffer pool 的时延。
这个技术 (Pointer swizzling - Wikipedia) 的本意是由于持久化保存(链表等数据结构的)指针逻辑地址没有意义,因为把逻辑地址写到磁盘里,但是再读出来的时候逻辑地址就什么也不是了,所以保存下一个 node 的 id 而不是地址值充当指针的作用,这个操作叫 unswizzling。在数据库中反其道而行之,如果 DBMS 确保都会在内存里操作,就可以专门存地址的原始值而不是 page id
因为树的高层结点使用频率非常高,它们 pin 在 buffer pool 里是常见的事情,这个技术使用场景比较多。
7.2.9 Write-Optimized B+Tree
在到达叶子节点之前,树的结构不发生任何改变
日志更改是增量级联改变


