Chapter 2: Transformer-based LLM

现在的大模型基本是 Transformer-based 的自回归预训练模型，本章我们将以 llama2 以及 GPT-3 为例介绍这种模型的基本结构。

Positional Encoding: RoPE
Attention: Multi-Head Attention or Multi-Query Attention or Grouped-Query Attention or Multi-Head Latent Attention or DeepSeek Sparse Attention
Normalization: LayerNorm or RMSNorm
FFN: MLP or SwiGLU or Mixture of Experts

Positional Encoding

一般分为两大类：绝对位置编码（Absolute Position Encoding）和相对位置编码（Relative Position Encoding）。本节将介绍这两种位置编码的区别及其重要性，并重点解析一种结合了两者优点的创新方法——旋转位置编码（Rotary Position Embedding, RoPE）

Why we need Position Encoding

在自然语言处理领域，Transformer 模型已成为一项革命性的技术。然而，其核心的自注意力机制本身并不具备捕捉序列中单词顺序的能力，即“位置无关性”。为了解决这一问题，位置编码应运而生。

绝对位置编码（Absolute Position Encoding）

给序列中的每个位置一个唯一的向量，把位置信息直接加到 token embedding 上。

固定式：不用学习参数，能推广到比训练时更长的序列在最初的 Transformer 论文《Attention Is All You Need》中，作者使用正弦和余弦函数来生成这些位置编码。其数学表达式如下：

$$ \begin{aligned} PE_{(pos, 2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\ PE_{(pos, 2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right) \end{aligned} $$

可学习式：模型可以学到适合任务的位置信息。训练时没见过的长序列可能无法泛化 $$ PE_{pos} = \text{Embedding}(pos) $$

相对位置编码（Relative Position Encoding）

相对位置编码是根据单词之间的相对位置关系来计算位置编码。这种编码方式更加灵活，能够捕捉到不同单词之间的相对位置信息，有助于模型更好地理解序列中单词之间的关系。但是也有缺点，计算效率低下，同时大部分相对编码都没有落地可行性。

Rotary Position Embedding (RoPE)

将位置编码与词向量通过旋转矩阵相乘，使得词向量不仅包含词汇的语义信息，还融入了位置信息

$$ (R_mq)^T(R_nk) = q^TR_m^TR_nk = q^TR_{m-n}k $$

给位置为 m 的向量 q 乘上矩阵$R_m$、位置为 n 的向量 k 乘上矩阵$R_n$用变换后的 Q,K 序列做 Attention，Attention 就自动包含相对位置信息

相对位置感知：使用绝对位置编码来达到相对位置编码的效果，RoPE 能够自然地捕捉词汇之间的相对位置关系。
无需额外的计算：位置编码与词向量的结合在计算上是高效的。
适应不同长度的序列：RoPE 可以灵活处理不同长度的输入序列。

目的

我们假设通过下述运算来给 q,k 添加绝对位置信息： [ \tilde{q}_m = f(q, m), \quad \tilde{k}_n = f(k, n) \tag{1} ]

也就是说，我们分别为 q,k 设计操作$f(\cdot,m),f(\cdot,n)$，使得经过该操作后，$\tilde{q}_m,\tilde{k}_n$就带有了位置 m,n 的绝对位置信息。Attention 的核心运算是内积，所以我们希望的内积的结果带有相对位置信息，因此假设存在恒等关系：

$$ ⟨f(q,m),f(k,n)⟩=g(q,k,m−n)\tag{2} $$

所以我们要求出该恒等式的一个（尽可能简单的）解。求解过程还需要一些初始条件，显然我们可以合理地设 $f(q,0)=q$ 和 $f(k,0)=k$

实现

位置 m 的编码进行解方程，我们得到二维情况下用复数表示的 RoPE：

$$ f(q, m) = R*f(q, m) e^{i \theta f(q,m)} = |q| e^{i(\Theta(q) + m\theta)} = qe^{im\theta} \tag{3} $$

矩阵形式：

$$ f(q, m) = \begin{pmatrix} \cos (m\theta) & -\sin (m\theta) \ \sin (m\theta) & \cos (m\theta) \end{pmatrix} \begin{pmatrix} q_0 \ q_1 \end{pmatrix} \tag{4} $$

由于内积满足线性叠加性，因此任意偶数维的 RoPE，我们都可以表示为二维情形的拼接，即

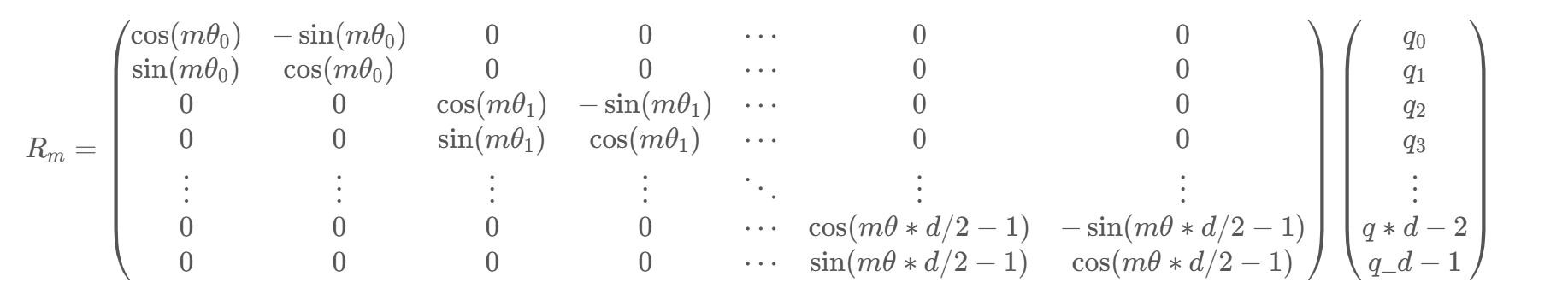:warning: 由于$R_m$具有稀疏性，不建议使用 matmul 进行实现，建议使用下面的方式实现：其中$\odot$是逐位对应相乘，即 Numpy、Tensorflow 等计算框架中的 ∗ 运算

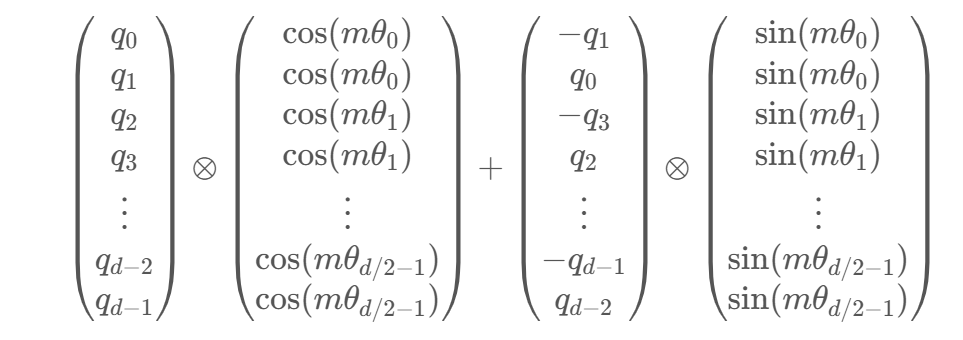
Attention Series

在 MHA (Multi Head Attention) 中，每个头有自己单独的 key-value 对；标准的多头注意力机制，h 个 Query、Key 和 Value 矩阵。
在 MQA (Multi Query Attention) 中只会有一组 key-value 对；多查询注意力的一种变体，也是用于自回归解码的一种注意力机制。与 MHA 不同的是，MQA 让所有的头之间共享同一份 Key 和 Value 矩阵，每个头只单独保留了一份 Query 参数，从而大大减少 Key 和 Value 矩阵的参数量。
在 GQA (Grouped Query Attention) 中，会对 attention 进行分组操作，query 被分为 N 组，每个组共享一个 Key 和 Value 矩阵 GQA 将查询头分成 G 组，每个组共享一个 Key 和 Value 矩阵。
- GQA-G 是指具有 G 组的 grouped-query attention。
  
  GQA-1 具有单个组，因此具有单个 Key 和 Value，等效于 MQA。而 GQA-H 具有与头数相等的组，等效于 MHA。

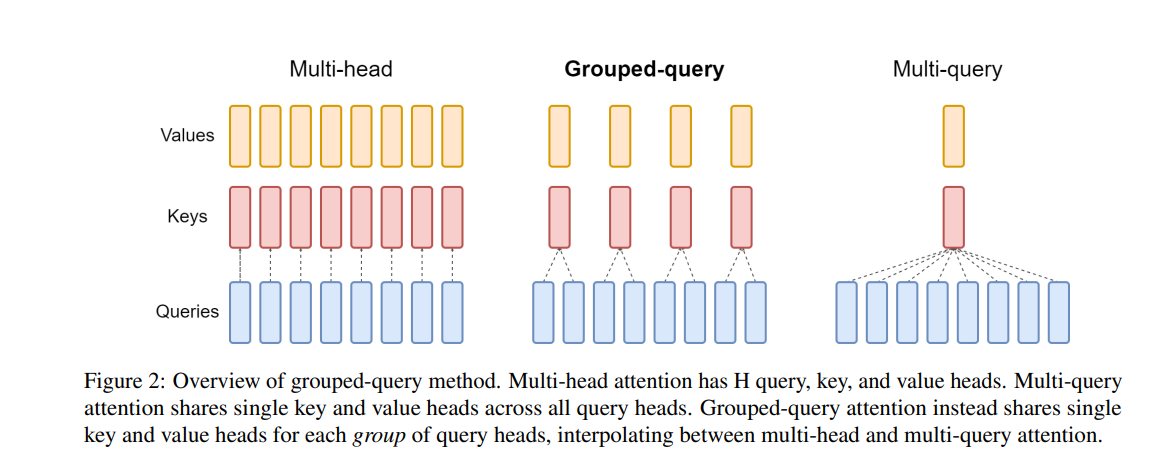
Multi-Head Latent Attention(MLA)

MLA 通过低秩联合压缩技术，减少了推理时的键值（KV）缓存，从而在保持性能的同时显著降低了内存占用

公式

在训练阶段，除了多了一步低秩投影以及只在部分维度加 RoPE 外，MLA 与 Q、K 的计算与 MHA 是基本相同的

RoPE 的$R_m$计算后投影矩阵与位置相关，为了解决这个问题，对 Q 和 K 的低秩投影分为两部分，一部分是原始的投影矩阵，另一部分是与位置相关的投影矩阵
在推理阶段，MLA 的计算可以等效为一个 MQA

投影矩阵吸收

在推理阶段，我们利用

$$ q_t^{(s)}k_i^{(s)T} = (x_tW^{(s)}_q)(c_iW^{(s)}_k)^T = x_t(W^{(s)}_qW^{(s)T}_k)c_i^T $$

将 $W^{(s)}_qW^{(s)T}_k$ 合并起来作为 Q 的投影矩阵，那么 $c_i$ 则取代了原本的 $k_i$，同理，在 $o_t$ 后面我们还有一个投影矩阵，于是 $v^(s)_i=c_iW^{(s)}_v$ 的 $W^{(s)}_v$ 也可以吸收到后面的投影矩阵中去，也就是说此时 KV Cache 只需要存下所有的 $c_i$ 就行，而不至于存下所有的 $k^{(s)}_i、v^{(s)}_i$。注意到 $c_i$跟$^{(s)}$无关，也就是说是所有头共享的，即 MLA 在推理阶段它可以恒等变换为一个 MQA。

RoPE 解耦

为 RoPE 是一个跟位置相关分块对角矩阵$R_m$，满足$R_mR^⊤_n=R_{m−n}$，MLA 加入 RoPE 之后会让固定的投影矩阵与位置相关：

$$ q^{(s)}_i=x_iW^{(s)}_qR_i,k^{(s)}_i=x_iW^{(s)}_kR_i $$

$$ q^{(s)}_tk^{(s)T}_i=(x_tW^{(s)}_q)(c_iW^{(s)}_k)^T = x_t(W^{(s)}_qR_{t-i} W^{(s)T}_k)c_i^T $$

这里的 $W^{(s)}qR{t-i} W^{(s)T}_k$ 就无法合并为一个固定的投影矩阵了（跟位置差 $t−i$ 相关），从而 MLA 的想法无法结合 RoPE 实现。

每个 Attention Head 的 Q、K 新增 $d_r$ 个维度用来添加 RoPE，其中 K 新增的维度每个 Head 共享：

$$ o_t = \big[o_t^{(1)}, o_t^{(2)}, \cdots, o_t^{(h)} ,\big] $$

$$ o_t^{(s)} = Attention!\left(q_t^{(s)}, k_{\le t}^{(s)}, v_{\le t}^{(s)}\right) = \frac{\sum_{i \le t} \exp!\left(q_t^{(s)} k_i^{(s)\top}\right) v_i^{(s)}} {\sum_{i \le t} \exp!\left(q_t^{(s)} k_i^{(s)\top}\right)} $$

$$ q_i^{(s)} = [x_i W_{qc}^{(s)},x_i W_{qr}^{(s)}R_i] ,\quad k_i^{(s)} = [c_i W_{kc}^{(s)},x_i W_{kr}R_i] ,\quad v_i^{(s)} = c_i W_v^{(s)}, \quad c_i = x_i W_c $$

Normalization

LayerNorm: 对某个样本的所有特征维度进行归一化

$$ \text{LayerNorm}(x) = \frac{x - \mu}{\sigma} \cdot \gamma + \beta $$
RMSNorm: 简化版的 LayerNorm，它不减去均值，只基于平方均值 (Root Mean Square) 来归一化 $$ \text{RMSNorm}(x) = \frac{x}{\sqrt{\frac{1}{d}\sum_{i=1}^{d} x_i^2 + \epsilon}} \cdot w $$

Why RMSNorm?

Layer-Norm 和 RMS-Norm 在测试集效果上没有明显差异，基本持平
RMS-Norm 的计算效率要更高

Feed Forward Network (FFN)

MLP: 两层全连接网络，中间使用非线性激活函数（如 ReLU 或 SiLU） $$ \text{FFN}(x) = \text{ReLU}(0, xW_1)W_2 $$
SwiGLU: 使用 SiLU 激活函数的变体并增加门控机制 $$ \begin{aligned} \text{SwiGLU}(x) &= (\text{Swish}(xW_1);\odot;xW_2) \ \text{Swish}(x) &= x \cdot \sigma(x) \end{aligned} $$
Mixture of Experts (MoE): 多个专家网络的集合，每个输入样本通过一个路由器选择部分专家进行处理，从而提高模型的表达能力
- Switch Transformer：Top-1 gating，每个 token 只去 1 个专家。
- GShard / GLaM：Top-2 gating，每个 token 走 2 个专家，结果加权。

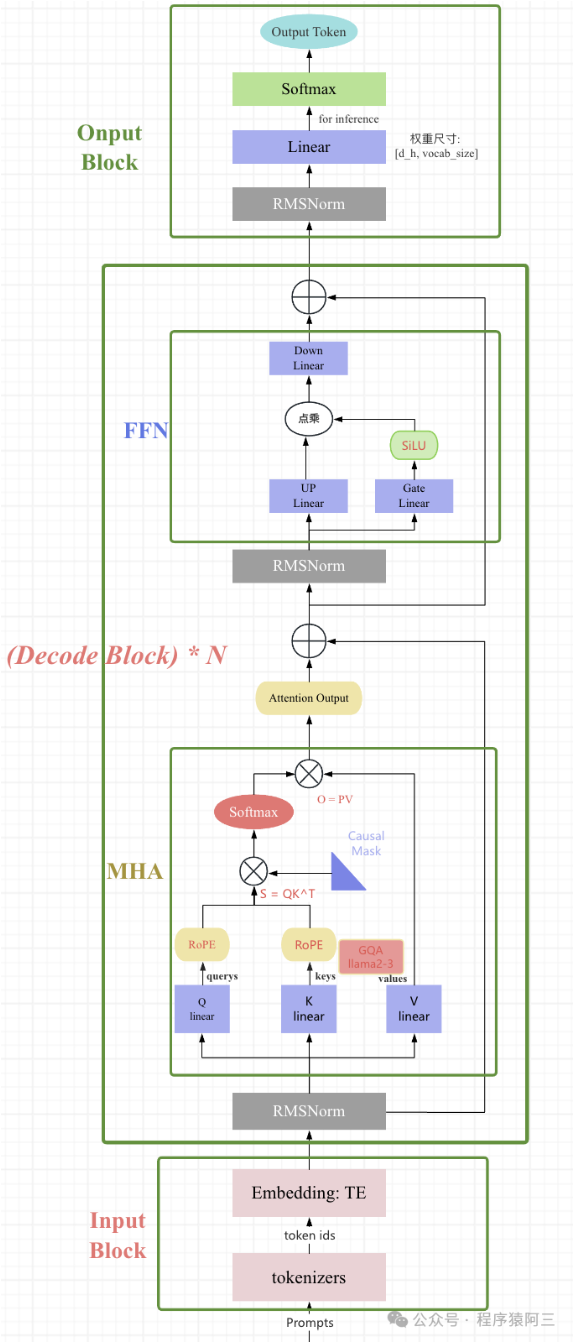
LLAMA2 模型结构

相较于 Transformer，llama2 使用了 pre-norm 结构
使用 RMSNorm 替代 LayerNorm，不计算样本均值
使用 Rotary Positional Encoding (RoPE)，用绝对编码的方式来实现相对位置编码
使用 GQA (Grouped-Query Attention)，平衡效率和性能
使用 SwiGLU 替代简单的 MLP，激活函数使用 SiLU

$$ \begin{aligned} \text{SwiGLU}(x) &= \text{Swish}(xW_1+b_1);\odot;(xW_2+b_2) \ \text{Swish}(x) &= x \cdot \sigma(x) \end{aligned} $$

LLM Study